Unbroken v0.6.187 - Boss Fight
Dev Diary: Update 6

“Hey, partner!
Adam here. Congratulations on your successful mission yesterday! I’ve watched the recordings of your ship’s front camera back and forth the whole night. Undeniably, you showed them who’s the boss, but I feel like we are missing something!
Didn’t you notice that most of the aliens aren’t really skillful or even decent pilots? It almost seems like they are mindlessly throwing their ships towards our cannons. Are they not afraid of death? What creeps me out even more is that they don’t chase us, when they have the advantage. They simply continue on their route, as if they have a bigger plan and we are just a mere annoyance, a couple of rocks in their way.
Their frigate ships certainly do seem a bit more thorough, though. Once we are within their sensor range, they stay and fight until the end. But even they don’t seem like they are getting nervous, when their hull is starting to crumble. Maybe they are not the brightest species. Or maybe there aren’t even living beings inside these ships. Nobody else seems to care, but I certainly do. I can’t help but believe that our enemy has an intricate plan for the invasion.”
Adam Pierce, Delta Squad Pilot, Unbroken Organization
Release Notes
Content Update
- new ship class: Piranha (Fighter Class)
- new wave: Piranhas shooting projectiles at an angle
Gameplay
- final boss will stay on screen and fight to the bitter end (cannot be evaded)
- final boss will now aim its weapons directly towards the player ship
UI
- damage gauge during boss fights, showing the remaining boss HP
Tech Talk
Fire weapons at an angle
Until now, projectiles moved only vertically across the screen. Therefore, we calculated the distance (s) as the projectile speed (v) times the time delta (t) and capped that distance at the projectile’s range. Then we moved the projectile either up or down the screen, depending on the projectile’s direction, which is +1 for projectiles being shot by the player ship and -1 for alien projectiles.

For this update, we want to allow for weapons to be aimed at certain angles, such that projectiles being shot from a weapon move along the very direction their parent weapon is pointing at. For that to happen, we can reuse our previous approach. But instead of moving the projectiles with a certain speed along the Y-axis, we now need to split the total projectile speed along the X- and Y-axes.
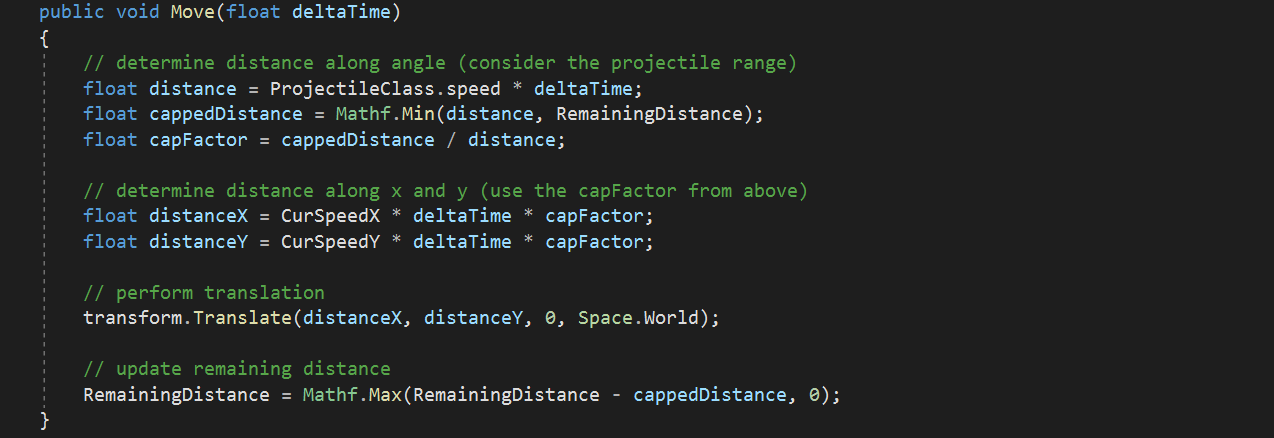
But how do we calculate the speed along the X- and Y-axes, if all we have is the total projectile speed (defined in ProjectileClassSO) and the target weapon angle? Trigonometry can answer this question for us.
Imagine we have two cannons equipped on a ship, each facing outwards at an angle α. For an example calculation, let’s concentrate only on the left-wing weapon and visualize the problem of finding the speeds along the X- and Y-axes as a right-angled triangle. For alien ships, since they are looking at the opposite direction, we simply add 180° to α.
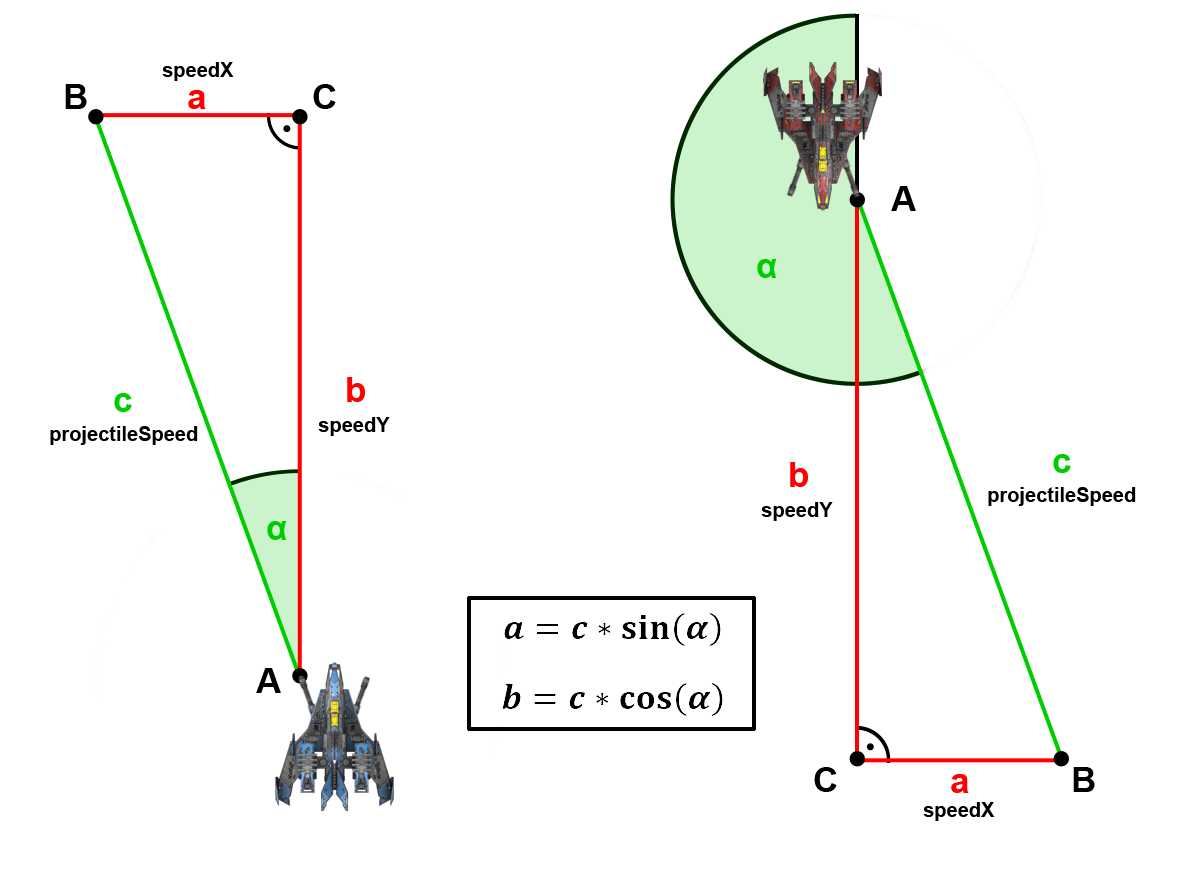
Given (marked green):
- the angle α for the player ship (= weapon angle)
- the angle α for an alien ship (= 180° + weapon angle)
- the length of c (= projectile speed)
Unknown (marked in red):
- the length of a (= speedX)
- the length of b (= speedY)
Solution:
Trigonometry offers the following formulas for calculating a and b:
- a = c * sin(α)
- b = c * cos(α)
Since trigonometry functions in Unity require the radian measure (RAD), we need to transform our DEG angles to RAD angles. RAD ranges from 0 to 2 Pi (= 6.28319) and DEG ranges from 0° to 360°. Hence, we can transform DEG to RAD by multiplying with 0.0174533.
Expectations:
- For weapons aimed left and up (from player perspective)
- which means DEG within (0°, 90°) and RAD within (0, 1/2 Pi)
- we expect projectiles to have
- negative speedX
- positive speedY
- For weapons aimed left and down (from player perspective)
- which means DEG within (90°, 180°) and RAD within (1/2 Pi, Pi)
- we expect projectiles to have
- negative speedX
- negative speedY
- For weapons aimed right and down (from player perspective)
- which means DEG within (180°, 270°) and RAD within (Pi, 3/2 Pi)
- we expect projectiles to have
- positive speedX
- negative speedY
- For weapons aimed right and up (from player perspective)
- which means DEG within (270°, 360°) and RAD within (3/2 Pi, 2 Pi)
- we expect projectiles to have
- positive speedX
- positive speedY
Example Calculation:
For the left-wing weapon of the player ship:
- projectile speed c = 5
- weapon angle α = 10° (DEG) = 0.174533 (RAD)
- a = c * sin(α)
- a = 5 * sin(0.174533)
- a = 0.868240 (= speedX)
- b = c * cos(α)
- b = 5 * cos(0.174533)
- b = 4.924038 (= speedY)
- Validation via Pythagorean theorem:
- c² = a² + b²
- 5² = 0.868240² + 4.924038²
- 25 = 0,753842 + 24,246158
- 25 = 25
For the left-wing weapon of the alien ship:
- projectile speed c = 5
- weapon angle α = 10° + 180° = 190° (DEG) = 3.31613 (RAD)
- a = c * sin(α)
- a = 5 * sin(3.31613)
- a = -0.868240 (= speedX)
- b = c * cos(α)
- b = 5 * cos(3.31613)
- b = -4.924038 (= speedY)
We’ll save us the validation, since the values differ only in the sign. And this is exactly what we would expect, since we have the same projectile speed and angle, just rotated by 180° for alien ships coming in from the top.
Results:
- player projectiles, fired at c = 5 and α = 10° will have
- a speedX of 0.868240 (move right)
- a speedY of 4.924038 (move up)
- alien projectiles, fired at c = 5 and α = 190° (10° + 180°) will have
- a speedX of -0.868240 (move left)
- a speedY of -4.924038 (move down)
Wait a second! Looks like the speedX values are just the opposite of what we stated in our expectations. A quick look at the graph below reveals that the sine function returns:
- a positive result for α values between (0, Pi)
- a negative result for α values between (Pi, 2 Pi)
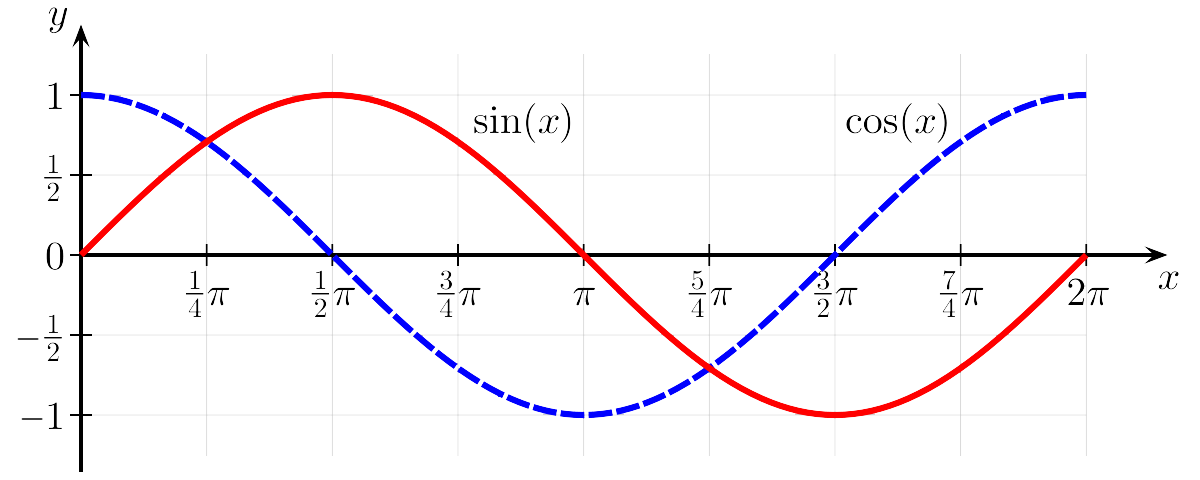
Fair enough. In order to get what we want, we can simply invert the sign of speedX after the calculation.
Implementation:
Let’s implement a Trigonometry class with static functions which we might want to reuse at some point in the future:
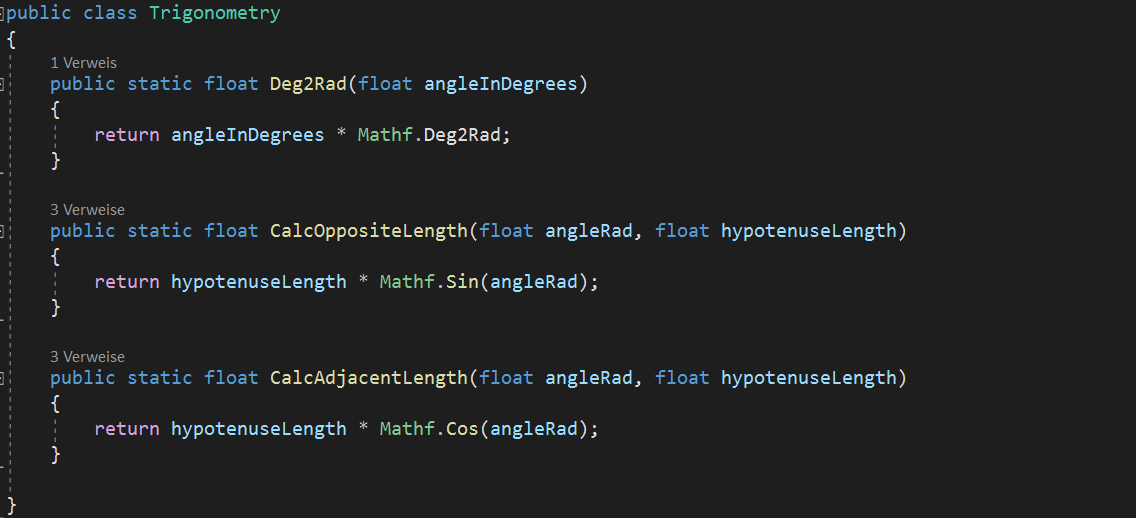
Finally, for our Move() method to work as expected, we need to initialize the CurSpeedX and CurSpeedY variables in the Init() method of our ProjectileController.
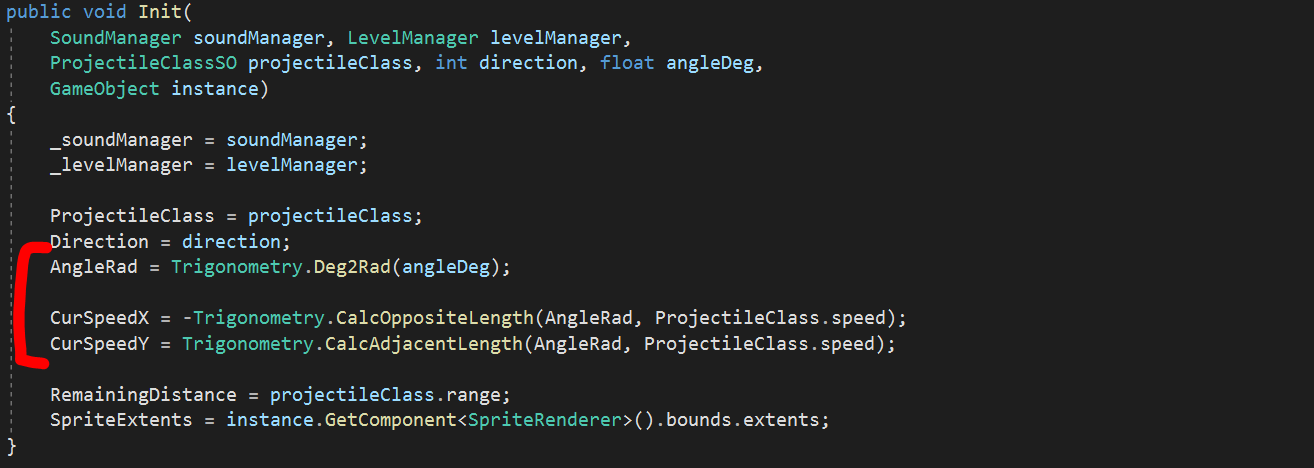
This is how it looks like when we define an angle for our weapons:

Get Unbroken - Mankind United
Unbroken - Mankind United
Defend Humanity against the Alien Invasion
| Status | In development |
| Author | Tobias Mielke |
| Genre | Action |
| Tags | 2D, Singleplayer, Space, Unity |
| Languages | English |
More posts
- Unbroken v0.7.264 - Modular Ship BuildingSep 06, 2022
- Unbroken v0.5.162 - Ship ModulesAug 06, 2022
- Unbroken v0.4.136 - Sounds GoodAug 05, 2022
- Unbroken v0.3.106 - Game Over?Aug 04, 2022
- Unbroken v0.2.74 - The Path to SuccessAug 03, 2022
- Unbroken v0.1.32 - First ContactAug 03, 2022
- Unbroken v0.1.16 - Endless SpaceAug 03, 2022
Leave a comment
Log in with itch.io to leave a comment.